Per chi cerca di applicare le sue conoscenze matematiche al mondo dell’economia e delle scienze sociali, offre interessanti spunti di riflessione la prefazione del professor Francesco Saraceno al volume di Mauro Gallegati “Il mercato rende liberi e altre bugie del neoliberismo”.

Coloro che hanno studiato approfonditamente la meccanica classica - quella di Newton, Lagrange, Hamilton - non potranno infatti che ritrovare parallelismi e analogie fra questa disciplina e l’economia mainstream. Non a caso gli economisti che hanno gettato le fondamenta dell’economia moderna, a cavallo tra l’800 e il ‘900, avevano spesso una formazione matematica o comunque tecnica, come Leon Walras (con studi di ingegneria).

Prendiamo, per esempio, il primo problema che si affronta in un corso di microeconomia: la scelta del consumatore. Tradotto in un linguaggio matematico, si tratta di ottimizzare la funzione di utilità dipendente dalle quantità dei beni nel paniere sotto il vincolo lineare di bilancio (il vincolo è formato da una combinazione lineare delle quantità, dove i coefficienti sono i prezzi). Matematicamente:

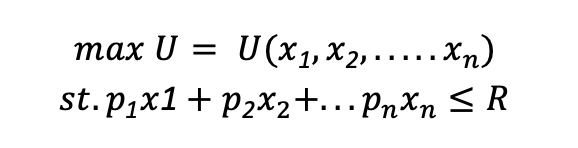
Un problema che, solitamente, si risolve in due modi: i matematici parametrizzano la retta vincolo inserendola nella funzione utilità (di fatto, il vincolo è attivo), gli economisti procedono con il metodo dei moltiplicatori di Lagrange.

Nella fisica classica l’ottimizzazione interviene in vari modi, ad esempio per trovare i punti di equilibrio di un corpo rigido, per l’appunto. Ma vi sono anche applicazioni più soddisfacenti per un matematico. Il principio variazionale di Hamilton, anche detto di minima azione, consiste nell’ottimizzazione non di una funzione, quanto di un funzionale: un’applicazione che agisce da uno spazio di funzioni a un campo, solitamente quello dei numeri reali.

E può essere tradotto in un sistema di equazioni differenziali, le equazioni di Eulero-Lagrange, equivalenti a quelle di Newton sotto determinate ipotesi.

Ma se in fisica agiamo in un sistema di riferimento che non influenza il comportamento degli enti che stiamo studiando, lo stesso non si può dire dell’economia. Come affermano Lesourne, Orlean, Walliser nel loro “Microeconomia Evoluzionista”, gli agenti economici della teoria mainstream agiscono in una Natura che è a loro indifferente.

Non solo: se in fisica l’ipotesi che le particelle siano omogenee, per usare un termine economico più comprensibile, è tutto sommato ragionevole, in economia la questione si complica. Gli agenti economici non possono essere considerati né omogenei né scollegati dalla natura, intesa ovviamente in senso lato, in cui operano.

Per far fronte a queste problematiche la teoria mainstream ha spesso cercato dei sotterfugi, alcuni anche ingegnosi. Tra questi vi è lo strumentalismo di Friedman, il cosiddetto as if. Non c’è dubbio che questa giustificazione sia affascinante. D’altronde è esattamente quello che si fa in fisica. Prendiamo la famosa legge di caduta dei gravi. Di sicuro si tratta di una legge che trascura molti aspetti del mondo reale. Se lanciamo un blocco di ghisa e una piuma da un grattacielo, la fisica ci dice che questi arriveranno a terra nello stesso momento muovendosi di moto rettilineo accelerato, indipendente dalla massa e seguendo la legge oraria:

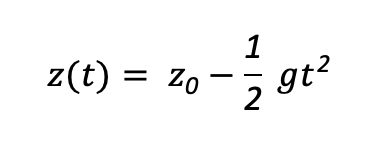
dove abbiamo supposto che partissero entrambi da fermi. In questo caso la realtà è un po’ più complessa: mentre la forma e la densità del blocco di ghisa lo rendono indifferente all’azione del vento e permettono di trascurare l’attrito dell’aria (di cui comunque si potrebbe tener conto usando equazioni leggermente più complesse), lo stesso non si può dire della piuma che verrebbe invece coccolata dal vento finendo per muoversi non più in modo rettilineo, ma in modo più complesso.

Tuttavia, la legge di caduta dei gravi ci permette di capire il fenomeno discretamente. Questa era la posizione di Friedman: non dobbiamo chiederci se il nostro modello tenga conto di tutti gli aspetti della realtà nel processo di modellizzazione, quanto se poi dà i risultati coerenti con le osservazioni empiriche.

Una posizione ancora più radicale è quella che vede nell’economia niente meno che una scienza dura al pari della matematica. Questa posizione, legittima, deve però essere abbracciata in toto se la si vuole adottare. La matematica, infatti, non si cura della realtà: è una scienza, come afferma Timothy Gowers, che studia come da determinate premesse si possa giungere a conclusioni seguendo regole e metodi che consideriamo universalmente validi.

Tuttavia, sconvolgere le premesse non rende una teoria matematica più o meno vera. Il risultato di 1+1 non è 2. In R e in altri campi o gruppi è 2. Ma in algebra tropicale dove l’operazione + è definita come il max tra i due numeri il risultato è 1. Se noi invece operiamo in algebra booleana il risultato sarà 0 (per chi ha più familiarità con la matematica, siamo in Z₂).

Di sicuro l’economia neoclassica ha raggiunto vette altissime, usando strumenti matematici non banali, come dimostrano appunto i lavori di Arrow e Debreu che fecero uso di strumenti topologici come i teoremi di punto fisso nei loro lavori.

Ma, se l’economia vuole tornare a parlare del mondo reale, deve, se non abbandonare la modellizzazione matematica adottata finora, quantomeno integrarla con modelli che più fedelmente descrivono il comportamento umano.

Anche e soprattutto nel campo della macroeconomia. Nonostante poi questa abbia cercato, nel corso degli anni ‘70 e fino ad oggi, di dare un fondamento microeconomico alla questioni macro, ci si è spesso limitati a considerare agenti con attributi distanti dalla realtà, ma soprattutto non si è studiato approfonditamente il rapporto che c’è tra gli agenti in termini non economici o, meglio, non razionali.

Nel mentre lo studio dei sistemi complessi si sta rivelando particolarmente fruttuoso in altri campi. Da ultimo quello dell’epidemiologia: basti pensare ai lavori di Alessandro Vespignani. Lo stesso si può dire nelle neuroscienze o nella biologia in generale.

Nella nostra lingua spesso usiamo “complicato” e “complesso” come sinonimi. Tuttavia, il significato di “complesso” è più complicato, per usare una battuta: i sistemi complessi sono quei sistemi dove il comportamento degli agenti dà luogo a proprietà emergenti.

Dal punto di vista economico questo significa indagare il comportamento degli agenti nelle loro interazioni anche non strettamente economico-razionali, concentrandosi sulle loro decisioni microeconomiche, abbandonando quindi una visione dell’agente rappresentativo e approdando a quello di agente eterogeneo. Lo studio della dinamica degli agenti porta quindi ad abbandonare l’idea dell’equilibrio generale, approdando a modelli multi equilibrio e di path dependence con fenomeni di isteresi.

Un fenomeno che si è indagato, riguardante un tema tanto sociale quanto economico, è quello della diffusione delle mode, studiato in “A Simple Model of Fads and Cascading Failures on Sparse Switching Networks”di Duncan J. Watts. Senza entrare molto nel tecnico: consideriamo una rete sociale, cioè un insieme di punti collegati da vertici. Questi punti hanno una caratteristica intrinseca: ogni punto può trovarsi nello stato 0 o nello stato 1. In un primo momento tutti i punti si trovano nello stesso stato, cioè 0.

Successivamente si assiste a una perturbazione, che può essere l’uscita di un libro o di un film o di una nuova linea d’abbigliamento. Quindi una frazione dei punti che formano la rete passa allo stato 1. Studiare la dinamica in una rete ideale, dove ogni agente è collegato egualmente agli altri, è abbastanza semplice. Vi sono infatti tre equilibri: tutti 1, tutti 0, e un equilibrio instabile, dove quindi non si verifica il fenomeno della cascata.

Ma i network reali sono sparsi. Non tutti gli agenti sono egualmente collegati agli altri. Nei network reali si formano dei cluster, cioè dei gruppetti. Sotto certe ipotesi sulla topologia, per cui si rimanda al paper citato, si può risolvere il problema facendo uso delle funzioni generatrici.

Questi metodi sono già presenti nella fisica e ampiamente applicati anche al mondo della sociodinamica. Il modello esposto poc’anzi rassomiglia al paradigma di Ising, nato in un primo momento per studiare l’andamento dello spin in un materiale che dà luogo o a ferromagnetismo o a paramagnetismo, e successivamente applicato a fenomeni reali come le dinamiche elettorali.

Per abbandonare quindi una visione estremamente semplificata che non tiene conto del ruolo delle istituzioni e delle interazioni non economico-razionali è necessario oltrepassare la modellizzazione marginalista e approdare a un’economia della complessità.